

The Nine Point Circle
By Leighton McIntyre
Goal: To construct the nine point circle and show how it relates to a triangle center.
Assignment 4:
Nine Point Circle Theorem
If ABC is any triangle, then the midpoints of the sides of triangle ABC, the feet of the altitudes of triangle ABC, and the midpoints of the segments joining the orthocenter of triangle ABC to the three vertices of triangle, ABC all lie on a single line.
A nine point circle can be constructed for any triangle. The nine significant points of the circle are:
- three side midpoints, one from each side of the triangle
- three altitude foot points, one from each foot of an altitude
- three segment midpoints, one from each segment of the vertex to the orthocenter of the triangle where the altitudes meet.
Constructing Nine Point Circle in GSP
1. Construct any triangle labeled ABC
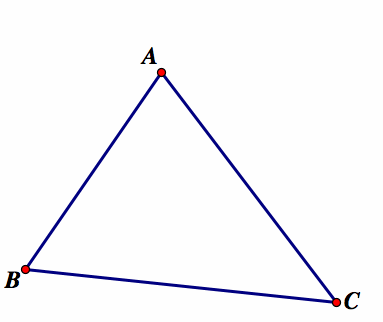
2. Construct the midpoints of each side AB, BC, AC. Label the midpoints D, E, and F
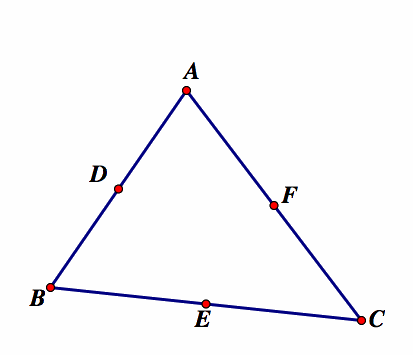
3. Construct the altitudes and label the feet of the altitudes R, S, and T.
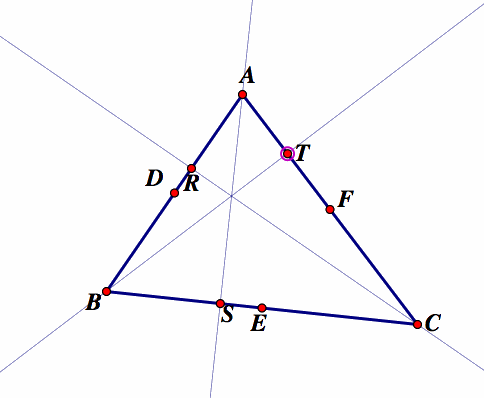
4. Label the point where all the three altitudes cross H. This is the orthocenter of the triangle.
5. Construct the midpoints of the segments AH, BH, CH. Label these points U, V, and W
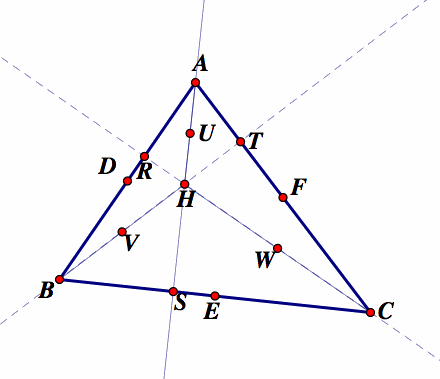
6. Construct the circumcenter (Q) of medial triangle DEF, this will serve as the center of the nine point circle.
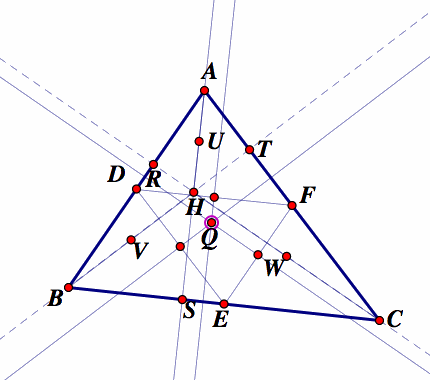
7. Construct the nine point circle using the center and any of the nine points.
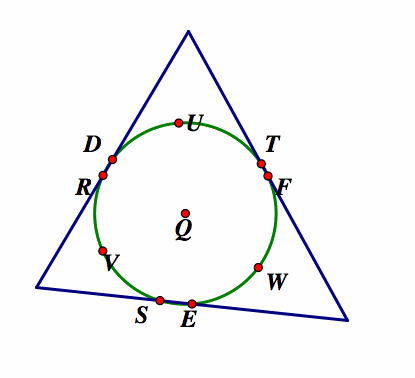
Investigate this GSP application to show how the circle always passes through the nine points. click here.
The Nine Point Center Theorem
The nine point center is the midpoint between the circumcenter and the orthocenter.
We now construct the circumcenter of the triangle ABC ( the orthocenter and nine point center were already constructed). We label this center O.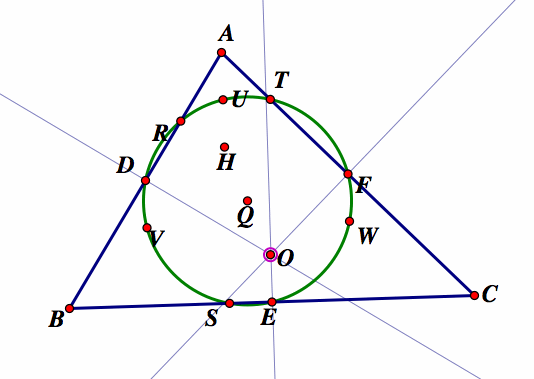
Now we can show this relationship between the triangle center using GSP.
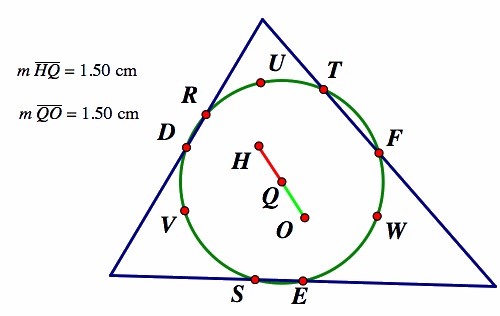
NOtice that the nine point center Q is halfway between the circumcenter (O) and the orthocenter (H) of the triangle. The distance HQ and distance QO are equal to each other.
We can see this in a better way using a GSP animation. Click here.